Overview
A hash table is a data structure which maps an element’s key to its value. The crux in the implementation of a hash table is its hash function, which, given an element’s key, computes the slot (or bucket) in the table where the element’s value is stored.
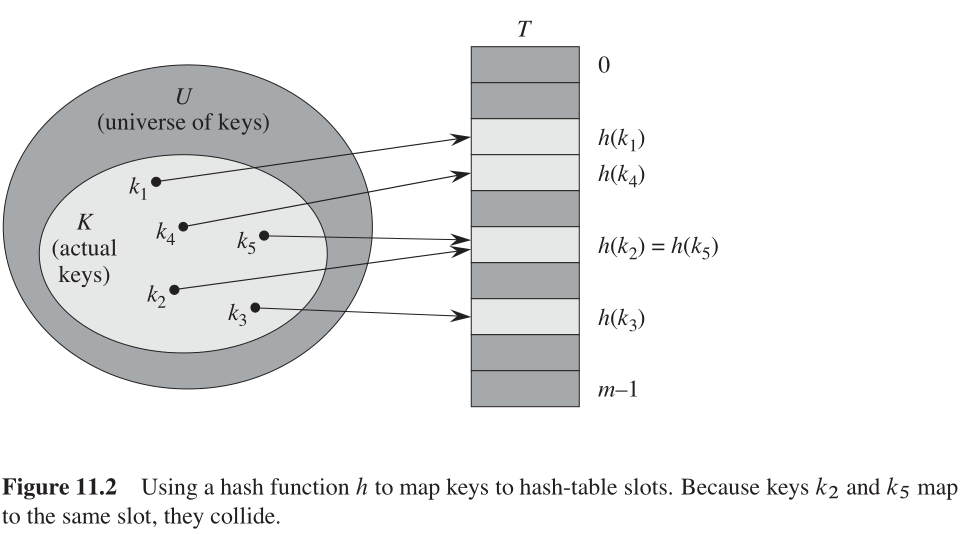(Source: [1])
In the picture, h() is the hash function which maps the key of an element to its slot index in the hash table T.
The main advantage of using hash tables is that they provide constant-time basic operations, e.g., insert, search, delete.
Properties of good hash functions
- Consistent: If given the same input, a hash function must always produce the same result. However, if a hash function produces the same result for two inputs, it does not mean the two inputs are the same.
- Efficient
- Uniform: The hash values produced by a hash function should be uniformly and independently distributed. One heuristic when designing a hash function is that the function should take into account every bit of information from its input.
Hash collisions and resolutions
A collision occurs when the hash function produces the same hash value for different items. This is because the set of possible hash values usually is smaller than the set of possible items, and also because it is difficult to make hash functions uniform in practice.
There are two popular approaches to deal with the collisions: open addressing and separate chaining.
Open addressing
Each slot holds at most one item. When collision happens, other slots are probed to see if they are available.
Linear probing
This probing sequentially probes the slots next to the colliding slot. For example, if a collision occurs at slot x, this probing sequentially probes slots x + 1, x + 2, x + 3, … until it finds a vacant slot.
Because linear probing puts items with same hash value next to each other, it tends to create clusters of those items. The presence of those clusters turns out to have negative impacts on the probing. First, clusters increase the chance of collisions because colliding items tend to fill up a whole section of the hash table. Second, as the number of items increases, clusters tend to get bigger and thus making probing time longer, because an entire cluster is probed whenever a collision occurs. This clustering problem is also referred to as primary clustering.
Quadratic probing
This probing quadratically probes other slots when collision occurs. The idea is to make the probe as wide as possible to avoid the primary clustering problem in linear probing. For example, if the collision occurs at slot x, this probing probes slots x + 1, x + 4, x + 9, … until it finds a vacant slot.
Since this probing deliberately avoid forming clusters from items with same hash value, it prevents the problem of primary clustering, but it suffers from another clustering problem called secondary clustering. This clustering problem is less severe than primary clustering. It does not make the colliding items fill up some section of a hash table and thus does not increase the chance of collisions. However, the probing time still increases as the number of items increases because, similar to linear probing, this probing uses fixed probe sequences.
Double hashing
Instead of using fixed probe sequences as in the previous probing methods, this probing method generates probe sequences by using an additional hash function. For example, if a collision occurs at slot x for the key k, this probing then probes slots x + h2(k), x + 2*h2(k), x + 3*h2(k), … until it finds a vacant slot, where h2(k) is the additional hash function. The idea of this probing method is to make the step-size of a probe sequence dependent on the key being probed on, so that different keys generate different probe sequences. As a result, this probing method does not suffer from the problem of increasing probing time caused by fixed probe sequences as in the other two probing methods.
The additional hash function should satisfy the following requirements:
- It is different from the primary hash function.
- It must not produce
0, otherwise it will cause endless loop of hashing.
A popular example of the second hash function is h2(k) = CONSTANT - (k % CONSTANT).
Separate chaining
With this kind of collision resolution, each slot in the hash table holds a reference to a list instead of a single item. When collision happens, the colliding element is simply put into the list at the corresponding slot.
Because each slot in the table points to a list, this resolution allows the load factor to be greater than or equal to 1, which is in contrast to open addressing where the load factor can be at most 1.
Compared to open addressing, separate chaining is more robust to the load factor in terms of the time it takes to resolve a collision. In open addressing, when the number of items increases, the probe sequence tends to get longer, and thus leading to a longer probing time. On the other hand, in separate chaining, regardless of the number of items, collision is always resolved by putting the colliding item into the corresponding chain.
References
[1] Introduction to algorithms
[2] Data structures and algorithms in Java