Definitions
A tree is a collection of nodes and edges without any cycle.
A search tree is a tree where each node is larger than nodes in its left subtree and smaller than nodes in its right subtree.
A multiway search tree is a search tree where each node contains multiple items and has multiple children.
An n-way search tree is a multiway search tree where each node has at most n children. For example, in a 2-way (or binary) search tree, each node has at most two subtrees, is larger than nodes in its left subtree, and is smaller than nodes in its right subtree.
B-Trees
B-trees are balanced multiway search trees, and thus are also considered as generalizations of red-black trees.
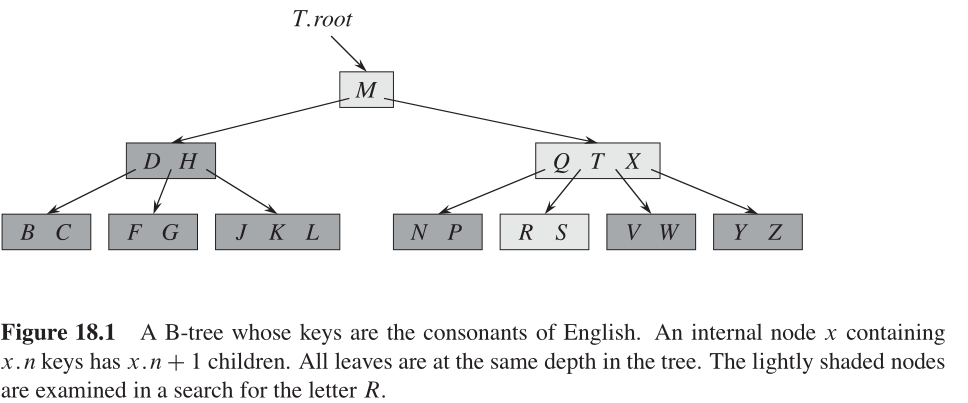(Source: Figure 18.1 [3])
Each node in a B-tree has an upper and lower bound on the number of items it can contain. Let say t is the minimum degree of a B-tree, then the number of items in each node (excluding the root) is in the range [t-1, 2t -1].
B-trees are especially suited for storing data in external storage, where the cost of accessing data is much more expensive than in the main memory. Two reasons for this suitability:
- Each node in a B-tree contains multiple items and is organized such that it fits into a block of data retrieved from each disk access. Thus, the number of disk accesses to get all necessary items is reduced.
- Because B-trees are balanced, its height is always kept to be a small value. Thus, the total number of disk accesses needed for basic operations (e.g., search, insert) are reduced. More specifically, the height of an B-tree is upper-bounded as follows [3]:
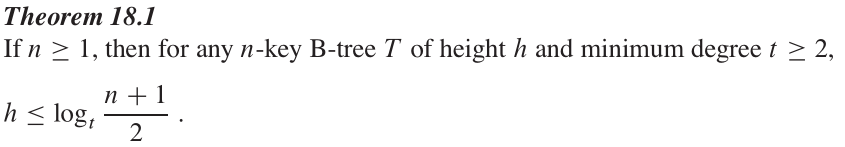
References
[1] https://en.wikipedia.org/wiki/K-ary_tree